Solving the Goldbox Crackme
Overview
Challenge Description

We are asked to enter a key, and the program checks to verify that the key is valid. There are many different valid keys for this challenge, so our goal is to not only find a single key, but to reverse engineer and replicate the validation algorithm.
You can find the challenge on GitHub here, or on crackmes.one here.
Anti-Disassembly
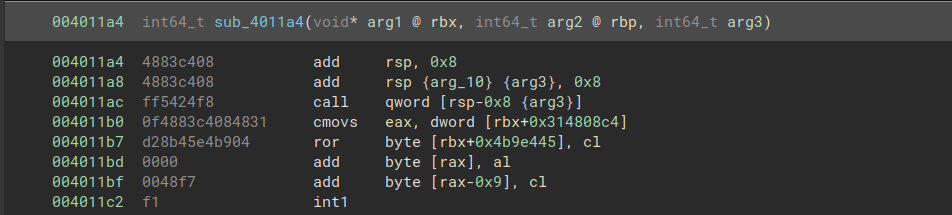
Looking at the disassembled code, we can immediately see sequences of instructions that don’t make sense. In this screenshot, all disassembly after the call instruction is incorrect. However, the function call shown here never returns, so the program never encounters the incorrect instructions.
There is another function with an entry point at 4011b1, but the disassembler fails to recognize it, as it has started disassembling a cmovs instruction at 4011b0. If we instead tell the disassembler to start at address 4011b1, we get a much more reasonable result:
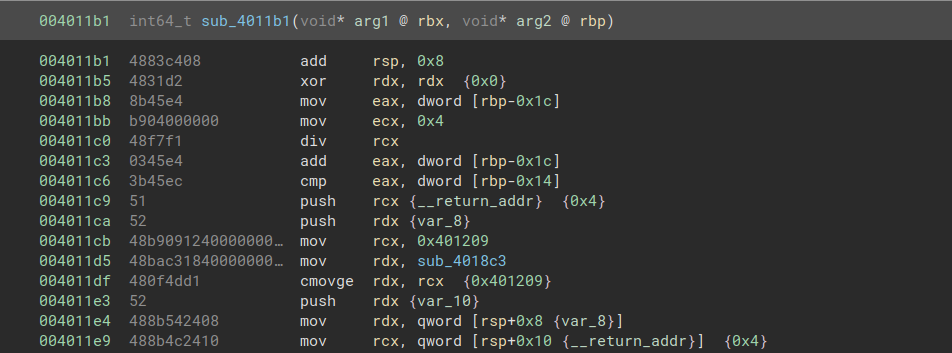
This anti-disassembly makes it nearly impossible to trace the control flow through static analysis. For the most part, I reconstructed the original control flow by stepping through the code in a debugger one instruction at a time.
The Key Format
We can immediately see a few basic checks being made. The first check verifies that the length of our key is 0x13:
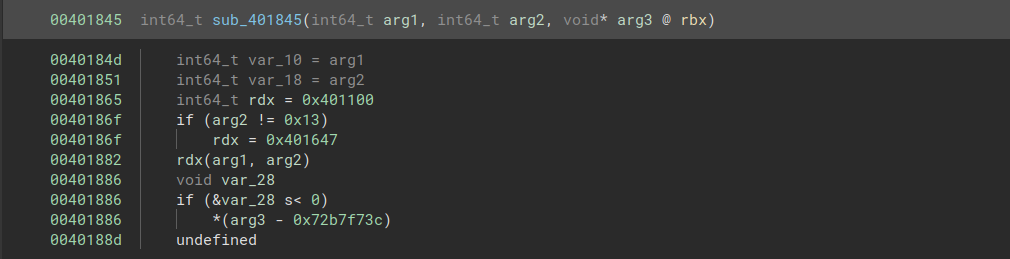
Subsequently, several characters are compared to the character -. This tells us that the key consists of 4 groups of 4 characters each, separated by dashes.

The First 8 Characters
I found that the first 8 characters were being compared to the characters in a long string. Initially, I thought that the key had to match the first 8 characters of this string, but on closer inspection I found that the program would accept any set of 8 characters that consisted only of letters appearing in the first half of the string (OFCKANLUPEQDHXTYWBMI).

The set of 8 characters that we choose from the first half of the string are used as the input for a validation function that determines the second 8 characters of our key. The second 8 characters are uniquely determined by this validation function: the program generates the remaining part of the key, then compares the rest of our input to it.
Technically, this is already enough to obtain a valid key. Since the program generates the entire key before comparing it to the input, we can just set a breakpoint in the debugger after the key is generated and read it from memory. This is how I approached the challenge initially, but then I went back and reverse engineered the validation function.
The Second 8 Characters
The Lookup Tables
The first thing the program does after checking the first 8 characters is to generate another 8-character string using values from the second half of the long string in the program’s memory. It turns out that long string is actually two separate lookup tables: the program finds the indices of the first 8 key characters in the first lookup table, then chooses the corresponding characters from the second lookup table.
For example, if we entered a key that began with OFCK-ANLU, the program would generate the string mqXagNiZ.
table1 = 'OFCKANLUPEQDHXTYWBMI'
table2 = 'mqXagNiZJWlEFSydocHP%#"'
def get_indices(key):
res = ''
for c in key: res += table2[table1.index(c)]
return res
The Hash Function
The newly generated string then has a series of transformations applied to it. Tracing through the program’s execution, I found that the string was being passed to a function that referenced the values 0xcbf29ce484222325 and 0x100000001b3. On closer inspection, I found that these values were actually constants hard-coded into the binary:

I Googled these values and found that they were used as the initial state of the FNV-1 hash function. Checking the output of the function in the binary, I verified that it was consistent with the FNV-1 hash of the string.
def fnv1_64(data):
state = 0xcbf29ce484222325
prime = 0x100000001b3
for i in data:
state = (state * prime) % 2**64
state ^= i
return state
This hash was then passed into a variation of the xorshift PRNG algorithm.

Fortunately, this was one of the few functions that actually had reasonable-looking decompilation, so it was pretty straightforward to replicate:
def xorshift(state):
mask = 0xffffffffffffffff
state ^= ((state << 0xd) & mask)
state ^= ((state >> 0x7) & mask)
state ^= ((state << 0x11) & mask)
return (state & mask)
The xorshift function was called 256 times, and the least significant byte was saved each time, leaving us with an array of 256 pseudorandom bytes.
The RC4 Encryption
I then found that a second 256-byte array was being generated. The obfuscated disassembly was particularly confusing in this stage, so rather than attempt to follow the control flow, I just stepped through the code and observed wnat was happening in memory.
I found that an array was being initialized with the values 0 to 255. The values in the array were then replaced with different values in order, one byte at a time.
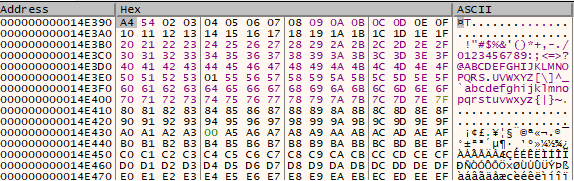
This was already enough to suggest to me that RC4 was being used. On closer inspection, I found that the first 256-byte array was being used as a key to derive the second array using RC4.
Generating The Key
Once the RC4 key is initialized, the program returns to the initial string that was used as input to the FNV-1 hash and encrypts it. At that point, the program returns to the xorshift function and generates more pseudorandom numbers, which are used to choose random indices into the RC4-encrypted string. Repeated indices are discarded, and the program continues to call the xorshift function until 4 distinct indices are produced:
indices = []
while len(indices) < 4:
res = xorshift(res)
if ct[res % 8] not in indices: indices.append(ct[res % 8])
The 4 resulting bytes are then used to index into the first 16 characters of the long string (OFCKANLUPEQDHXTY), creating a new string of 8 capital letters.

second_key = ''
short_table1 = table1[0:0x10]
for i in indices:
second_key += short_table1[i % 0x10]
second_key += short_table1[(i // 0x10) % 0x10]
These 8 capital letters are expected to be the second 8 characters of our original input. If the input does not match these 8 characters, then our key is invalid.
Putting all of this together, we finally have a keygen script:
from Crypto.Cipher import ARC4
table1 = 'OFCKANLUPEQDHXTYWBMI'
table2 = 'mqXagNiZJWlEFSydocHP%#"'
def get_indices(key):
res = ''
for c in key: res += table2[table1.index(c)]
return res
def fnv1_64(data):
state = 0xcbf29ce484222325
prime = 0x100000001b3
for i in data:
state = (state * prime) % 2**64
state ^= i
return state
def xorshift(state):
mask = 0xffffffffffffffff
state ^= ((state << 0xd) & mask)
state ^= ((state >> 0x7) & mask)
state ^= ((state << 0x11) & mask)
return (state & mask)
first_key = input(f"Enter any 8 characters from the following table: {table1}\n")
table2_key = get_indices(first_key).encode('utf-8')
res = fnv1_64(table2_key)
n = 256
lsb_arr = b''
for i in range(n):
res = xorshift(res)
lsb_arr += (res & 0xff).to_bytes(1, 'little')
cipher = ARC4.new(lsb_arr)
ct = cipher.encrypt(table2_key)
indices = []
while len(indices) < 4:
res = xorshift(res)
if ct[res % 8] not in indices: indices.append(ct[res % 8])
second_key = ''
short_table1 = table1[0:0x10]
for i in indices:
second_key += short_table1[i % 0x10]
second_key += short_table1[(i // 0x10) % 0x10]
final_key = f"{first_key[0:4]}-{first_key[4:8]}-{second_key[0:4]}-{second_key[4:8]}"
print(f"Generated key {final_key}")